In recent years, the sheer amount of data of systems has grown substantially, to the extent it becomes too large for a single machine to hold, therefore process. Out of the necessity enforced by existing hardware capabilities, in order to store all information, it is distributed among many smaller machines (servers, nodes, etc), and are broadcasted upon requests when a query or a computation needs to be made.

This approach is not only wasteful with regard to energy consumption, since broadcasting requires power, but also renders the system insecure; it is important to keep the data private and unavailable to third parties that may be listening.

The popular solution is to transmit a different value, that represents the data, and is much smaller. It is energy-efficient and secure, since even by seeing it, the data cannot be recovered. The challenge is to extrapolate a meaningful approximation from that value; for problems which it can be done, we can solve without looking at the entire data, which is our main goal here.

This research is conducted under the supervision of Prof. Daniel Keren (Homepage), whose specialties include: Analyzing and monitoring large data streams, especially in a distributed setting & Applications of Polynomials. Large data streams (particularly in distributed or dynamic settings) directly imposes on this research field, and is an approach to handle the very same challenges raised in the introduction of this blog. Polynomials are used for numerical optimizations, which is the second aspect of this research; the art of finding solutions closer to the ideal solution, for problems in which the ideal solution cannot be found due to the limits of computation.

Example of Notable Results:

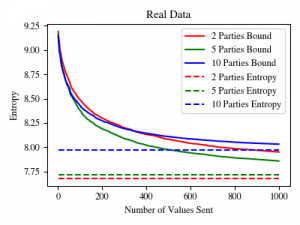Entropy bound of a distributed system by number of values sent (dotted line is the real value). A graph showing the performance of an algorithm suggests in the paper published in Entropy (see Papers), and used to bound from above the entropy of a distributed vector.

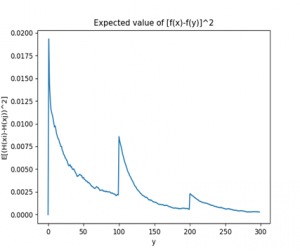Detection of “distant” points (the spikes in the graph), by the scalar value transmitted. An algorithm suggested by the paper submitted to ITCS (see Papers), which clearly shows when an “outlier” sample is added to the stream, a probability based solution to a known difficult problem.

For more information, see:

Communication Efficient Algorithms for Bounding and Approximating the Empirical Entropy in Distributed Systems

A Fast and Reliable Solution to PnP, Using Polynomial Homogeneity and a Theorem of Hilbert